Investimentos / Fundos - Uma Introdução à Teoria do Investimento
Capítulo I: Mercados de Capital e Performance de Investimento
Resumo
Suponha que você encontre uma grande oportunidade de investimento, mas falta
caixa para tirar proveito dela. Este é um problema clássico de financiamento.
Uma resposta curta é aquela em que você empresta - ou privativamente de um
banco, ou publicamente distribuindo títulos. Títulos nada mais são do que
promessas de pagamentos futuros. Eles são inicialmente lançados através de
intermediários financeiros tais como bancos de investimentos, que subscrevem a
oferta e trabalham para vender os títulos ao público. Uma vez vendidos, os
títulos podem freqüentemente ser em comprados novamente. Existe um segundo
mercado para muitos títulos de corporações. Se eles satisfizerem a certas
exigências reguladoras, eles podem ser comercializados por corretores nas bolsas
de valores, tais como a NYSE, a AMEX, a NASDAQ e a BOVESPA ou nas trocas de
opções e nas mesas de negócios de bonds.
Os títulos entram numa desconcertante variedade de formas - existem mais
tipos de títulos do que existem raças de gatos e cães, por exemplo. Eles
abrangem dos relativamente simples ao incrivelmente complexos. Um straight bond
promete pagar sobre um empréstimo uma quantidade fixa de juros durante um tempo
e o principal na maturidade. Um estoque de ações, por outro lado, representa uma
fração da posse de uma corporação, e uma exigência de dividendos futuros. Hoje,
muito da inovação em finanças é o desenvolvimento de títulos sofisticados: notas
estruturais, reverse floaters, IO's e PO's -- estes são hoje raças
especializadas. Fontes de informações sobre títulos são numerosas na world-wide
web. Para começar, veja o Ohio State Financial Data Finder. Todos os títulos, do
mais simples ao mais complexo, tem alguma semelhança básica que permite-nos
avaliar sua utilidade da perspectiva do investidor. Todos eles são exigências
econômicas contra benefícios futuros. Ninguém pede emprestado dinheiro para
reembolsá-lo imediatamente; a dimensão do tempo está sempre presente nos
instrumentos financeiros. Assim, um bond representa a exigência de uma série
futura de pagamentos pré-fixados, enquanto uma ação representa exigência de
futuros dividendos incertos e divisão dos ativos da corporação. Ainda mais,
todos os títulos financeiros podem ser caracterizados por duas características
importantes: risco e retorno. Estas duas medidas chaves serão
focalizadas neste segundo módulo.
I. Finanças da Perspectiva dos Investidores
A maioria das decisões financeiras que você se dirigiu até este ponto foi em
termos da perspectiva da empresa. A companhia deveria empreender a construção de
uma nova planta de processamento? É mais lucrativo substituir uma caldeira velha
agora, ou esperar? Neste módulo, nós examinaremos decisões financeiras da
perspectiva do comprador de títulos corporativos: os acionistas e bondholders
que são livres para comprar ou vender ativos financeiros. Investidores, se eles
são indivíduos ou instituições tais como fundos de pensão, fundos mútuos, ou
fundações universitárias, mantém portfólios, isto é, elas mantém uma
coleção de diferentes títulos. Muito da inovação em pesquisa de investimento
durante os últimos 40 anos foi o desenvolvimento de uma teoria de administração
de portfólio, e este módulo é principalmente uma introdução a estes novos
métodos. Ele responderá à pergunta básica: Que taxa de retorno exigirão os
investidores para segurar um título arriscado na seus portfólios? Para
responder a esta pergunta, temos primeiro que considerar o que os investidores
querem, como nós definimos retorno, e o que nós queremos dizer com o risco.
II. Por que os Investidores Investem
O que motiva uma pessoa ou uma organização comprar títulos, ao invés de gastar o
seu dinheiro imediatamente? A resposta mais comum é a economia -- o desejo de
passar o dinheiro do presente para o futuro. As pessoas e organizações antecipam
as necessidades de caixa futuras, e esperam que seus ganhos no futuro não
satisfarão aquelas necessidades. Uma outra motivação é o desejo de aumentar o
valor, i.é, fazer o dinheiro crescer. Às vezes, o desejo para ficar rico no
futuro pode fazer você querer assumir riscos grandes. A compra de um bilhete de
loteria, por exemplo somente aumenta a probabilidade de ficar muito rico, mas às
vezes um desconto pequeno num pagamento grande, até mesmo se valer um dólar ou
dois, é melhor do que absolutamente nada. Há outros motivos para investimentos,
é claro. Caridade, por exemplo. Você pode estar disposto a investir para fazer
acontecer algo, caso contrário, que não poderia acontecer--você poderia investir
na construção de um museu, financiar moradores de baixa-renda, ou reivindicar
bairros urbanos. Os dividendos destes tipos de investimentos podem não ser
econômicos, e por isso eles são difíceis de comparar e avaliar. Para a maioria
dos investidores, metas caridosas aparte, a medida fundamental de benefício
derivada de um título é a sua taxa de retorno.
III. Definição de Taxas de Retornos
O retorno do investidor é uma medida do crescimento da riqueza que resulta
daquele investimento. Esta medida de crescimento é expressada em termos de
porcentagem para torná-la comparável por investidores grandes e pequenos. Nós
expressamos freqüentemente o porcentual de retorno sobre um intervalo de tempo
específico, digamos, um ano. Por exemplo, a compra de uma parte de ações no
instante t, representado como Pt levará a P t+1 após uma
ano, assumindo que não serão pagos nenhum dividendo. Este retorno é calculado
como: R t = [ P t+1 - Pt]/ Pt. Note
que isto é algebricamente o mesmo que: Rt= [P t+1/ Pt]-1.
Quando os dividendos são pagos, ajustamos os cálculos para incluir o pagamento
do dividendo intermediário: Rt=[ P t+1 - Pt+Dt]/
Pt. Enquanto isto leva em consideração todos os pagamentos
explícitos, há outros benefícios que podem aparecer ao se manter uma ação,
incluindo o direito para votar nas assembléias da corporação, tratamento de
imposto, direitos de doações, e muitas outras coisas. Estes são refletidos
tipicamente na flutuação de preço das ações.
IV. Taxas de Retornos Aritmética vs. Geométrica
Existem duas medidas comumente lembradas do retorno médio: as médias, geométrica
e aritmética. Elas raramente concordam uma com a outra. Considere um exemplo de
dois períodos: P0 = $100, R1 = -50% e R2
= +100%. Neste caso, a média aritmética é calculada como (100-50)/2 = 25%,
enquanto a média geométrica é calculada como: [(1+R1)(1+R2)]1/2-1=0%.
Bem, você fez, ou não, dinheiro nos dois períodos? Não, você não fez, assim a
média geométrica está mais próxima da experiência do investimento. Por outro
lado, suponha que R1 e R2 fossem representativos
estaticamente dos retornos futuros. Então no próximo ano, você terá uma chance
de 50% de obter $200 ou uma chance de 50% de obter $50. Se retorno esperado de
um ano é (1/2)[(200/100)-1] + (1/2)[(50/100)-1] = 25%. Desde que a
maioria dos investidores tem um múltiplo horizonte anual, o retorno geométrico é
útil para avaliar o quanto seu investimento crescerá a longo prazo. Entretanto,
em muitos modelos estatísticos, a taxa aritmética de retorno é empregada. Para
tratabilidade matemática, assumimos um horizonte de período único para o
investidor.
V. História do Mercado de Capitais
Os anos 1980's foi uma das maiores décadas para os investidores em ações na
história do mercado de capitais dos U.S.A.
(Courtesia Ibbotson Associates)
Medimos a performance do mercado de ações pelo retorno total do investimento
na S&P 500, que é um índice padrão de 500 ações, com pesos estabelecidos pelo
valor de mercado do patrimônio líquido da empresa. Os dividendos pagos pelas
empresas S&P 500 são assumidos serem investidos novamente em ações. Isto
estabelece uma medida do retorno total do investidor, antes dos impostos
individuais serem pagos.
A década de 1930 foi uma das piores décadas para os investidores de ações dos
U.S.A.
(Courtesia Ibbotson Associates)
Na década de 1930 o mercado de ações quebrou totalmente em todo
globo. Os investidores de ações dos U.S.A. experimentaram um retorno de zero por
cento por um período de onze anos de 12/1929 a 12/1939.
O Mercado de Capitais dos U.S.A. sobre um Longo Prazo: 1926 - 1995
Por mais de 68 anos, um investimento em ações no S&P aumentou de $1 a $800
(Courtesia de Ibbotson Associates)
VI. Prêmio do Risco
Note na figura anterior que um dólar investido em ações cresceu para $889 no
período, enquanto um dólar investido em bônus da empresa cresceu até $40. Por
que a grande diferença? Este retorno diferencial é comumente atribuído à
diferença no risco associado com ações em oposição aos bônus. Note que a linha
de ações é "mais trêmula" do que a linha de bônus. A riqueza investida em ações
desde 1926 foi mais volátil do que a riqueza investida em bônus. A
despeito disso quanto maior o retorno, maiores também os riscos. Um investidor
tipicamente deve ter cuidado sobre o perigo de um investimento. Se, por exemplo,
você está economizando para comprar uma casa em algum instante no próximo ano,
então você deve ter realmente cuidado se seus $100.000 de pé-de-meia tem
uma probabilidade significante de cair para $50.000 em doze meses. Como um fato
importante, você poderia estar disposto a negociar uma taxa mais baixa de
retorno de investimento por "segurança" de que seu principal será mantido. Isto
é chamado de aversão ao risco -- e sendo todas as coisas iguais, a
maioria dos investidores preferem menos risco do que mais.
Sumário Estatístico dos Investimentos dos U.S.A. de
1926 até Março, 1995. Fonte: Ibbotson Associates
| Investimento |
média geom. |
média aritmét. |
desvio-padrão |
retorno alto |
retorno baixo |
| Retorno total do S&P |
10.30 |
12.45 |
22.28 |
42.56 |
-29.73 |
| U.S. Small Stock TR |
12.28 |
17.28 |
35.94 |
73.46 |
-36.74 |
| U.S. LT Govt TR |
4.91 |
5.21 |
8.00 |
15.23 |
-8.41 |
| U.S. LT Corp. TR |
5.49 |
5.73 |
7.16 |
13.76 |
-8.90 |
| U.S. 30 day T-Bills |
3.70 |
3.70 |
.96 |
1.35 |
-0.06 |
A diferença entre o retorno total da S&P e o do T-Bill de 30 dias dos U.S.A. é
chamada de prêmio de equity. É a quantia de retorno que os investidores
demandam para manter um título de risco tal como ações, em oposição aos títulos
sem risco, tal como o T-Bills. O prêmio de equity anual é cerca de 9%
aritmético, e 6% geométrico, durante o período de 1926 - 1995.
VII. Desvio Padrão como uma Medida do Risco
Lucros acionários podem ser mais arriscados ou mais voláteis, mas este conceito
é difícil para simplesmente se expressar. Para fazer isto, nós pedimos
emprestado um conceito de estatística, chamado desvio padrão. O desvio
padrão é uma medida sumária sobre o espalhamento médio das observações. É a raiz
quadrada da variância, que é calculada como:

O desvio padrão de um ano dos retornos da S&P 500 é cerca de 22,28%. Se os
retornos S&P são normalmente distribuídos, isto significa que cerca de 2/3 da
vezes nós observaríamos um retorno anual dentro do intervalo (12,45-22,28)=
-9,93 e (12,45+22,28)= 34,73. Um histograma dos retornos anuais da S&P 500
mostra que os retornos são aproximadamente, ou são mesmos, distribuídos
normalmente? Uma distribuição normal permitiria retornos inferiores a -100%.
Ações não fazem isso. De fato, o log da variável que está sendo
distribuída normalmente é uma aproximação melhor. Entretanto, há evidências para
sugerir que mesmo isto não é tão certo. As caudas dos lucros acionários são um
pouco " mais gorda " do que deveria ser observado se os retornos fossem
distribuídos log-normalmente. Isto proporciona um pouco de apoio à
hipótese avançada por Benoit Mandelbrot de que os lucros acionários seguem uma
distribuição "estável", com variância indefinida. Dê uma olhada ao histograma
S&P 500:

Quão bem o desvio padrão captura a noção de risco do investidor? Pesa igualmente
os lucros altos com baixos lucros. Isto influencia pesadamente as observações
extremas. Não está relacionado à forma da distribuição. Todas estas são críticas
válidas. Porém os benefícios para usar desvio padrão são grandes. É uma única
medida, permitindo-nos quantificar retornos de ativos através do risco. Como nós
veremos no próximo capítulo, ela também provê a base para decisões do investidor
sobre a escolha de portfólio.Capítulo II: A Geografia da Fronteira Eficiente
No capítulo anterior, nós vimos como o risco e o retorno de investimentos podem
ser caracterizados por medidas de tendência central e medidas de variação, i.e.
média e desvio padrão. Na realidade, a estatística é o fundamento das finanças
modernas, e virtualmente todas as inovações financeiras dos últimos trinta anos,
amplamente denominadas " Teoria do Portfólio Moderno" , foi baseada em modelos
estatísticos. Por causa disto, é útil revisar o que é uma estatística, e como
ela se relaciona ao problema de investimento. Em geral, uma estatística é uma
função que reduz uma grande quantia de informação a uma quantidade pequena. Por
exemplo, a média é um número único que resume a "localização" típica de um
conjunto de números. A estatística reduz muita informação a alguns números
úteis--como tal, eles ignoram uma grande transação. Antes da teoria do portfólio
moderna, a decisão sobre se incluir um título em uma carteira estava
principalmente baseada na análise fundamental da empresa, suas demonstrações
financeiras e sua política de dividendo. O professor de finanças Harry Markowitz
começou uma revolução sugerindo que o valor de um título para um investidor
poderia ser avaliado melhor por sua média, seu desvio-padrão, e sua correlação a
outros títulos da carteira. Esta sugestão audaciosa chegou a ignorar muita
informação sobre a empresa--seus salários, sua política de dividendo, sua
estrutura de capital, seu mercado, seus competidores--e calculando algumas
poucas estatísticas simples. Neste capítulo, seguiremos nós a direção de
Markowitz e veremos onde a tecnologia da teoria de portfólio moderna nos levará.
I. O Risco e o Retorno dos Títulos
A grande perspicácia de Markowitz era que as informações relevantes sobre os
títulos podem ser resumidas através de três medidas: a média do retorno (tomada
como a média aritmética), o desvio-padrão dos lucros e a correlação com os
outros retornos dos ativos. A média e o desvio-padrão podem ser usados para
delinear o risco relativo e o retorno de qualquer seleção de títulos. Considere
seis classes de ativos:
(Cortesia Ibbotson Associates)
Esta figura foi construída usando o risco histórico e dados de retorno das Small
Stocks, ações S&P, Bonds Corporativos, Bonds do Governo, e um índice acionário
internacional chamado MSCI, ou Morgan Stanley Capital International World
Portfólio. A figura mostra a dificuldade que um investidor enfrenta face a qual
ativo escolher. Os eixos do gráfico delineiam o desvio-padrão anual de lucros
totais, e a média anual dos retornos do período 1970 até 3/1995. Note que ações
pequenas provêem o retorno mais alto, mas com o risco mais alto. Em qual classe
de ativos escolheria você para investir seu dinheiro? Há qualquer classe única
de ativos que domina o resto? Note que um investidor que prefere uma baixa
estratégia de risco escolheria T-Bills, enquanto um investidor que não se
preocupa com risco escolheria Small Stocks. Não há nenhum título que seja melhor
para TODOS os investidores.
II. Portfólios de Ativos
Tipicamente, a resposta para o problema de investimento não é a seleção de um
ativo acima de todos os outros, mas a construção de uma carteira de ativos, i.e.
diversificação por vários títulos diferentes. A chave para diversificação está
na correlação dos títulos. Lembre-se da análise de dados e estatísticas que o
coeficiente de correlação é um valor entre -1 e 1, e mede o grau de co-movimento
entre duas variáveis aleatórias, neste caso os lucros de ação. É calculado como:

Onde o sigma AB é a covariância dos dois títulos. Aqui está como usar a
correlação no contexto da construção do portfólio. Considere dois títulos, A e
B. O título A has uma média de 10% e um desvio-padrão de 15%. O título B tem uma
média de 20% e um desvio-padrão de 30%. Podemos calcular o desvio-padrão de um
portfólio composto de diferentes misturas de A & B usando esta equação:

O retorno médio não é tão complicado. É uma simples média ponderada das médias
dos dois ativos:
médiap = W A RA + W B R B.
Note que um portfólio terá tipicamente um peso de um, assim usualmente, W A
+ W B = 1.
O que acontece se a correlação de A&B = 0 ? Note que uma
carteira de 80% A e 20% B tem um desvio padrão de: of: sqrt(0,82*0,152+0,22
0,32+2*0*0,8*0,2*0,15*0,3) = 13,4 %
Em outras palavras, a mistura de 20% dos TÍTULOS DE MAIORES RISCOS realmente
diminuem a volatilidade da carteira! Este é um resultado notável. Ele significa
que você pode reduzir o risco e aumentar o retorno pela diversificação dos
ativos.
O que acontece se a correlação de A&B = 1 ? Neste caso, a perfeita
correlação entre os dois ativos significa que não existe diversificação. O
desvio padrão da carteira de um mix de 80/20 é 18%. Isto é igual a combinação
linear dos desvios padrões: (.8)(.15)+(.2)(.30) = 18%
O que acontece se a correlação de A&B = -1 ? Este é um caso não
usual, porque significa que quando A move-se para cima, B sempre move-se para
baixo. Tome uma mistura de 0,665 A e(1-0,665) B. sqrt(0,6652*0,152+(1-0,665)20,32+2*0*(0,665)*(1-0,665)*0,15*0,3)
= 0,075%, que está muito próximo de zero. Em outras palavras, A é
aproximadamente um perfeito hedge para B. Umas das poucas correlações negativas
da vida real que você encontrará é a short position de ações compensando a the
long position. Neste caso, desde que os retornos médios também são os mesmos, o
retorno esperado será zero. Estes extremos dos valores da correlação permite-nos
descrever um envelope dentro do qual todas as combinações dos dois ativos
cairão, apesar de suas correlações.

(Cortesia Campbell Harvey)
III. Mais Títulos e Mais Diversificação
Agora considere o que acontecerá quando você põe mais ativos na carteira. Tome o
caso especial no qual a correlação entre todos os ativos é zero, e todos eles
tenham o mesmo risco. Você achará que pode reduzir o desvio padrão da carteira
misturando vários ativos em lugar de apenas dois. Cada ponto representa uma
combinação de ativos igualmente ponderada; de uma única ação para duas, para
três, para trinta, e mais. Note que, depois de 30 ações, a diversificação na
maior parte é atingida. Há ganhos enormes para diversificação além de uma ou
duas ações.

(Cortesia Campbell Harvey)
Se você se permitir variar os pesos da carteira, em lugar de os manter igual, os
benefícios serão maiores, porém a matemática é mais desafiadora. Você não só tem
que calcular o desvio padrão da mistura entre A&B, mas o desvio padrão de toda
mistura concebível dos títulos. Não obstante, se você fizer assim, você achará
que há um conjunto de carteiras para as quais provêem o mais baixo nível de
risco para cada nível de retorno, e o nível mais alto de retorno para cada nível
de risco. Considerando todas as combinações de ativos, um conjunto especial de
carteiras sobressairá--este conjunto é chamado de fronteira eficiente.

A fronteira eficiente, mostrada em azul, é o conjunto de dominantes, pelo menos
da perspectiva de um investidor averso ao risco. Para QUALQUER nível de risco, a
fronteira eficiente identifica um ponto que é a carteira de retorno mais alta na
sua classe de risco. Justamente por isso, para qualquer nível de retorno, a
fronteira identifica a carteira de mais baixo de risco naquela classe de
retorno. Note que ela extende da carteira de retorno máximo (geralmente um único
ativo) à carteira de variância mínima. A fronteira eficiente tem uma carteira
para todo mundo -- existem infinitos números de pontos no conjunto,
correspondendo às variações infinitas nas preferências dos investidores ao
risco. A área chamada conjunto provável representa todas as combinações
prováveis de ativos. Não existem ativos que ficam de fora do conjunto provável.
IV. Markowitz e a Primeira Fronteira Eficiente
A primeira fronteira eficiente foi criada por Harry Markowitz, usando um punhado
de ações da New York Stock Exchange. Aqui está ela, reproduzida do seu livro
Portfólio Selection Cowles Monograph 16, Yale University Press, 1959. Ela
tem uma linha indo para a origem, porque Markowitz estava interessado nos
efeitos da combinação dos ativos de risco com os sem risco: caixa.
![[FRONTIER]](http://www.igf.com.br/imagens/artigos/6626-12.gif)
Note, também, que é inclinado para o seu lado. A convenção do Desvio-Padrão
sobre o eixo X é desenvolvida mais tarde.
V. Uma Fronteira Eficiente Real Hoje
Esta figura é uma fronteira eficiente criada dos depósitos históricos dos U.S.A.
e ativos internacionais durante o período de 1970 até 3/1995, usando o programa
Ibbotson EnCorr Optimizer.

(Cortesia Ibbotson Associates)
Isto é o estado de arte da tecnologia de seleção de carteiras, entretanto
ainda está baseado no programa de otimização original de Markowitz. Existem
algumas características básicas para se lembrar:
- Uma variância mínima de carteira existe
- Uma carteira de retorno máximo é composta de um único ativo.
- B,C,D & E são pontos críticos em que um dos conjuntos de ativos
usados na fronteira muda, i.é, um ativo cai fora ou entra naqueles
pontos.
- Não existe ativos a noroeste da fronteira. Por isso é que chamamo-la
de fronteira. É o limite das combinações prováveis de riscos e retornos.
VI. A Fronteira Eficiente com os Ativos Sem Risco
T-Bills são freqüentemente tomados como ativos sem riscos, e seu retorno é
indicado como R f, a taxa livre de risco. Uma vez que você permite
combinar o ativo sem risco em uma carteira, a fronteira eficiente pode
mudar. Considerando que é sem risco, ele não tem nenhuma correlação aos
outros títulos. Assim ele não fornece diversificação, per se. Ele
fornece uma oportunidade para ter uma carteira de baixo risco, entretanto.
Esta figura é um diagrama da fronteira eficiente composta de TODOS os ativos
de risco na economia, como também dos ativos sem riscos.
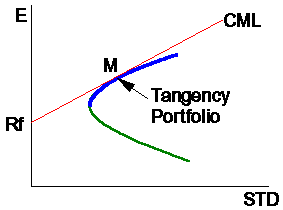
(Cortesia Campbell Harvey)
Neste caso especial, a nova fronteira eficiente é um raio,
estendendo de Rf ao ponto de tangência (M) com a fronteira "ativo de risco"
eficiente, e daí por diante. Esta linha é chamada a Capital Market Line (CML). É
de fato um conjunto de carteiras investíveis, se você pudesse pedir emprestado e
emprestar à taxa sem risco! Todas as carteiras entre Rf e M são carteiras
compostas de contas de tesouraria e M, enquanto todas as carteiras à direita de
M são geradas PEDINDO EMPRESTADO à taxa sem risco Rf e investindo os rendimentos
em M.
VII. Sumário
O modelo de Markowitz foi uma inovação brilhante na ciência de seleção de
carteira. Com quase um toque de mão desarmada, Markowitz mostrou para nós que
todas as informações necessárias para escolher a melhor carteira para qualquer
determinado nível de risco está contido em três estatísticas simples: média,
desvio -padrão e correlação. Parece de repente que você nem mesmo precisou de
qualquer informação fundamental sobre a empresa! O modelo não requer nenhuma
informação sobre política de dividendo, salários, ação de mercado, estratégia,
qualidade de administração--nada sobre a miríade de coisas com que os analistas
de Wall Street se interessam! Em resumo, Harry Markowitz fundamentalmente
alterou como as tomadas de decisões de investimento eram feitas. Virtualmente
todo gerente de carteira principal hoje consulta um programa de otimização. Eles
podem não seguir exatamente as suas recomendações, mas eles usam isto para
avaliar risco básico e o retorno de transações.
Por que todo o mundo não usa o modelo de Markowitz para resolver os seus
problemas de investimento? A resposta está novamente nas estatísticas. O retorno
médio histórico pode ser uma estimativa pobre do retorno médio futuro. Quando
você aumenta o número de títulos, você aumenta o número de correlações que você
tem de calcular--e você os tem que calcular obter a resposta certa CORRETAMENTE.
Na realidade, com mais de 1.500 ações no NYSE, alguém está certo em achar
correlações que são largamente inexatas. Infelizmente, o modelo não se trata bem
com as contribuições incorretas. Isso é por que é melhor aplicado a decisões de
distribuição por classes de ativos para as quais o número de correlações é
baixo, e os sumários estatísticos são bem estimados.
|