Ações / Bolsa de Valores - Modelos Pós-Black & Scholes 

Muitas pesquisas foram realizadas visando testar o modelo de Black & Scholes, porém, ele ainda continua sendo a base para muitos modelos. Apesar das diferenças verificadas entre os preços de mercado e os preços dados pelo modelo, estas diferenças têm sido pequenas quando comparadas aos custos operacionais.

Uma das tentativas foi o trabalho de MERTON (1976): os retornos da ação-objeto seguem um processo de difusão e saltos de Poisson. Generaliza o modelo para o caso de taxas de juros estocásticas, em ocasiões onde o prazo até o vencimento de opção é longo e as taxas de juros são voláteis. Esta adaptação é fundamental para outros ramos das finanças, como, por exemplo, análise de investimentos, onde o prazo até o vencimento é longo e incerto.

Seguindo o modelo de Black & Scholes, Merton mostra que o valor da opção aumenta continuamente na medida em que t (tempo), r (taxa de juros) ou v (volatilidade) aumentam. Em cada um destes casos, o limite superior é o preço da ação.

Argumenta que o valor da opção é sempre maior do que seria se ela fosse exercida imediatamente. Sendo assim, um investidor racional só exerceria sua opção de compra no vencimento, concluindo-se, então, que o valor fornecido pela fórmula aplica-se também a opções de compra do tipo americano. Com pequenas modificações, a fórmula aplica-se a opções de venda do tipo europeu.

O autor ainda mostra que o valor de uma opção de venda do tipo americano será sempre maior do que o de uma do tipo europeu, pois há sempre a possibilidade concreta do exercício antes do vencimento. Isso implica na não adequabilidade da fórmula de Black & Scholes para a precificação deste tipo de opção

Sobre o assunto, primeiro MERTON (1976) propõe um modelo no qual a taxa de juros é uma variável estocástica. Em seguida, MERTON (1976) e COX e ROSS (1976) derivam uma equação para o caso em que a evolução do preço da ação-objeto apresenta uma componente descontínua.

Admitem, explicitamente, a descontinuidade da distribuição dos retornos da ação-objeto. É admitida a existência de dois componentes distintos que causam diferentes variações no preço da ação.

O componente contínuo, responsável pelo reflexo dos desequilíbrios temporários entre oferta e demanda e a chegada de novas informações gerais sobre a economia, é modelado segundo um processo padrão de Wiener.

O componente discreto, ou por saltos, que reflete a chegada de novas informações específicas sobre a ação ou o setor em que atua, é modelado por um processo de Poisson, com taxa 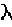, que reflete o número de saltos por unidade de tempo.

MERTON (1976) argumenta que, apesar da ocorrência de saltos, a criação de uma proteção (hedge) neutra é possível, desde que se forme uma carteira suficientemente diversificada, pois o componente de saltos tem origem num risco não-sistemático, ou diversificável.

Segundo RODRIGUES (1990), vários testes empíricos foram feitos para comparar a qualidade da avaliação obtida pelo modelo de Merton em contraste com a obtida pelo modelo original de Black & Scholes. Constata-se que, apesar de mais "refinado" em relação ao modelo original, a proposta de Merton não se revelou adequada, pois a diferença entre os dois modelos a nível de precisão nos resultados obtidos é mínima.

No caso das opções sobre ações que pagam dividendos, tem-se uma tentativa de aprimorar o modelo de Black & Scholes, já que o mesmo não considera o pagamento de dividendos. COX e ROSS (1976) alegam que os retornos da ação-objeto seguem um processo de difusão e saltos de Poisson. THORPE (1976) examina os efeitos da restrição às vendas a descoberto. Junto com Merton (1976), modifica o modelo para o caso de a ação-objeto pagar dividendos.

Em outra tentativa, GESKE e JOHNSON (1984) derivaram uma fórmula para a precificação de opções do tipo americana.

PRESS apud CANABARRO (1988) propõe estudo em que é fundamental a determinação de um modelo que descreve o comportamento dos preços da ação-objeto com mais precisão do que o modelo de distribuição lognormal. Ele divide o processo de formação dos retornos em duas partes, tendo um modelo híbrido de distribuições, contendo um componente normal e um componente binomial: a primeira parte é um componente de difusão contínua, sendo uma função dos desequilíbrios temporários entre oferta e demanda, e da chegada das informações genéricas sobre o mercado; a outra é um componente descontínuo, caracterizado por saltos, que correspondem à chegada de novas e importantes informações específicas sobre a ação-objeto ou o setor em que esta se situa.

Para CHO e FREES (1988), o processo nunca é contínuo. Analisam estimativas de volatilidade quando a evolução do preço da ação é discreta, encontrando vieses em relação à proposta de continuidade. Sendo assim, o movimento da ação-objeto é híbrido, porém híbrido de uma distribuição discreta e um componente também discreto, por saltos.

RENDLEMAN e BARTTER (1979) elaboram um modelo e o chamam de dois estados, que é uma derivação algébrica da idéia da proteção (hedge) neutra, não tão elegante matematicamente, porém simples e eficaz.

Seu pressuposto básico é que o preço da ação-objeto variará num determinado intervalo de tempo, de um montante H+, no caso da variação ser para cima, ou H-, caso em que a variação seria para baixo.

Para RODRIGUES (1990) o modelo é generalista e extremamente simples, pois se se associar a distribuição de probabilidades correta para a magnitude da variação de preço da ação, ou seja, ao se estimar corretamente o valor esperado da distribuição dos preços da ação-objeto, seja ele contínuo ou discreto, tem-se uma opção avaliada corretamente. Uma grande vantagem é sua aplicação quando o processo de formação de preços do ativo-objeto é binomial, e num caso limite quando é normal (pois, como se sabe, a distribuição normal é um caso limite da binomial).

Para situações ex-post, o modelo fornece o exato valor da opção, porém para situações onde não se conhece o valor esperado da magnitude da mudança do preço, torna-se necessário estimar-se subjetivamente.

A abordagem geral para precificação de derivativos elaborada por HULL (1989) é estruturalmente similar com a equação diferencial desenvolvida por Black & Scholes. Apenas faz a inclusão de algumas variáveis desconsideradas no modelo base.

HULL (1991) cita que para entender os preços futuros do mercado a termo e mercado futuro é conveniente dividi-los em duas categorias: aqueles cujo objeto de negociação é mantido para investimento por um número significativo de investidores - as traded securities; e aqueles cujo objeto de negociação é possuído basicamente para consumo. Considera ações, bonds, ouro e prata como traded securities, todavia taxa de juros, taxa de inflação e commodities não são.

No caso dos ativos de consumo, não é possível obter preços futuros como uma função do preço a vista e de outras variáveis perceptíveis. Um parâmetro como custo de oportunidade do ativo torna-se importante, já que mede até que ponto os usuários da mercadoria (commodity) consideram as vantagens de possuir o ativo físico, que não são obtidas por detentores de um contrato futuro. Tais vantagens podem incluir a capacidade de realizar lucro com escassez temporária ou de manter um processo de produção em andamento. Através de teorias de arbitragem, é possível obter apenas um limite superior para os preços futuros de ativos de consumo.

Para HULL (1991), as teorias de arbitragem permitem que os preços a termo e futuro de contratos de ativos para investimento sejam determinados com precisão, em função do preço a vista e de outras variáveis conhecidas. Porém, isso já não é possível para os preços de derivativos de ativos de consumo.

O modelo de Black & Scholes é relativamente complexo. No entanto, é mais completo, pois tem embutido em sua rationale o modelo de distribuição dos preços da ação-objeto.

A maioria das instituições financeiras usa os modelos matemáticos de Black e Sholes e Binomial, que servem basicamente para traduzir o comportamento dos preços dos derivativos frente aos preços no mercado a vista (spots).