A operação de proteção (hedging), que parece à primeira vista uma
transação simples, merece algumas ponderações.
HULL (1994) cita que muitos participantes dos mercados futuros buscam
proteção, e utilizam os derivativos para reduzir determinado risco que possam
enfrentar, relacionados ao preço do petróleo, a uma taxa de câmbio, ao nível do
mercado de ações. Uma proteção (hedge) perfeita, que na prática é rara, é
aquela que elimina completamente o risco.
Pretende-se discorrer nesta parte do trabalho sobre alguns caminhos pelos
quais a proteção (hedge) pode ser conduzida, de modo que sua eficácia
seja a mais perfeita possível, ou seja, mostrar quais são as posições que uma
empresa pode tomar para neutralizar o risco tanto quanto possível.
A proteção (hedge) pode ser de venda ou de compra. Uma proteção (hedge)
de venda, por exemplo, pode ser feita por um produtor de soja, que colocará o
produto à venda em dois meses; já um hedge de compra torna-se necessário
quando uma empresa tem de adquirir determinado produto no futuro e deseja fixar
um preço hoje.
Um dos problemas que surge na eficácia da proteção (hedge),
concentra-se em alguns problemas:
Risco de base:
Base é igual ao preço à vista do ativo a ser protegido (hedgeado) - preço
futuro do contrato utilizado.
A escolha do contrato futuro que será utilizado para a proteção (hedge)
é um dos fatores que afeta o risco da base, possuindo dois componentes (HULL,
1991):
1. a escolha do ativo-objeto do contrato futuro; é necessário fazer
uma análise detalhada para determinar qual dos contratos futuros disponíveis
possui preço o mais correlacionado possível com o preço do ativo a ser protegido
(hedgeado);
2. a escolha do mês de vencimento: o ideal é escolher um mês de
vencimento que esteja o mais próximo possível do vencimento da proteção (hedge),
sem ultrapassr essa data.
Razão da proteção (hedge):
Um outro fator responsável pela dificuldade na determinação da proteção (hedge)
é a razão de proteção (hedge), ou seja, a razão entre o tamanho da
posição em contratos futuros e a extensão do risco.
O problema de determinação da razão de proteção hedge surge do fato de
que os preços em ambos os mercados, ou seja o preço à vista da mercadoria e o
preço do mercado futuro, não apresentam idênticas variações.
Para GOMES (1987), os preços nos mercados à vista e futuro são imperfeita e
positivamente correlacionados. Mesmo que os preços fossem perfeitamente
correlacionados, as respectivas variações absolutas não seriam necessariamente
idênticas, e este aspecto é de fundamental importância na determinação do risco
da proteção (hedge) e, consequentemente, da razão de proteção (hedge).
Este problema, passa pela questão da definição dos objetivos da proteção (hedge).
Conclui que a proteção (hedge) não afeta somente o risco, mas também o
retorno associado à posição mantida e existe uma relação de troca entre ambos.
As teorias de proteção (hedging), que discorrem sobre a razão
de proteção (hedge), podem ser classificadas em dois grandes grupos,
segundo a ênfase dos modelos que empregam, de acordo com GOMES (1987):
a) sobre risco: teoria clássica e teoria minimizadora;
b) sobre o risco-retorno: teoria da especulação na base e teoria do
portfólio.
Na Teoria Clássica, para cada quantidade de mercadoria mantida no mercado a
vista, o protetor (hedger) deve manter a mesma quantidade na posição
oposta estabelecida no mercado futuro; isto é, deve empregar uma razão de
proteção (hedge) igual à unidade. Logo, o risco só é eliminado se os
preços em ambos os mercados forem perfeita e positivamente correlacionados, e
apresentarem idênticas variâncias, condições raras de serem encontradas.
Conforme WARD E SCHIMKAT (1979), o hedger não é capaz ou não deseja
formar expectativas acerca do movimento dos preços e seus lucros derivam
exclusivamente de algum processo de "transformação" da mercadoria, qualquer que
seja (estocagem ou produção de outra mercadoria).
A Teoria Minimizadora postula o emprego de uma razão de proteção (hedge)
correspondente ao beta da mercadoria (coeficiente angular da reta que associa os
preços do mercado a vista aos do mercado futuro). Possui condições restritivas,
embora menos que as exigidas pela teoria clássica.
A principal crítica a estas duas teorias é que não levam em consideração o
retorno esperado de proteção (hedge).
A Teoria da Especulação na Base parte do pressuposto que, usualmente, o risco
da proteção (hedge) não pode ser completamente eliminado e propõe a sua
administração ativa para aumentar os retornos. Se a diferença entre o preço a
vista e o preço futuro for expressiva, deve-se efetuar a proteção (hedge)
para, em seguida, desfazê-la, realizando os correspondentes lucros quando essa
diferença diminuir significativamente, e assim sucessivamente.
Segundo WORKING (1953), essa abordagem considera a possibilidade de se
aumentar o retorno através da proteção (hedging) seletiva ou especulação na
base, decorrentes das variações relativas entre os preços nos mercados a vista e
futuro.
Para GOMES (1987), pode-se destacar duas questões dessa teoria: a primeira é
a dificuldade de determinar-se quando a base é significativamente grande ou
pequena; a segunda está relacionada com o fato de que entre transações
sucessivas o protetor (hedger) pode ficar exposto aos riscos de
flutuações adversas nos preços da mercadoria no mercado a vista.
De acordo com a teoria da Carteira de Investimentos (portfolio),
existirá uma única razão ótima de proteção (hedge) independentemente da
estrutura de preferências do protetor (hedger), já que este poderá
satisfazer suas preferências quanto ao risco através da adequada divisão do
investimento entre o ativo livre de risco e a proteção (hedge) ótima.
Para determinar essa razão ótima de proteção (hedge), basta maximizar
a função objetivo (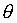 )
definida por LINTNER (1965):
)
definida por LINTNER (1965):
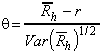 .
.
E a razão ótima de proteção (hedge) (h*) será dada por:
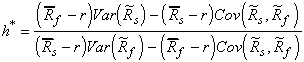
onde: 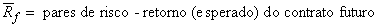 ;
;
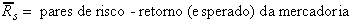 ;
;
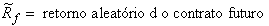 ;
;
 ;
;
Para GOMES(1987), a teoria da Carteira de Investimentos (Teoria do
Portfolio) parece ser superior às teorias clássica e minimizadora, por
considerar de forma sistemática o risco e o retorno da proteção (hedge) à
luz da estrutura de preferências do protetor (hedger). Tendo em vista que
a teoria da especulação na base propõe um modelo dinâmico de proteção (hedge),
não pode ser comparada com as demais. Entretanto, é importante notar que é a
teoria que mais se aproxima do comportamento efetivo dos agentes econômicos.
HULL (1994) afirma que não é ideal utilizar uma razão de proteção (hedge)
de 1,0. Se o protetor (hedger) desejar minimizar a variância de sua
posição total, uma razão de proteção (hedge) diferente de 1,0 será mais
apropriada. Através de algumas considerações matemáticas, o autor determina que
razão de proteção (hedge) ideal é a inclinação da linha de eficiência
máxima quando as mudanças no preço a vista são regredidas contra as mudanças no
preço futuro.